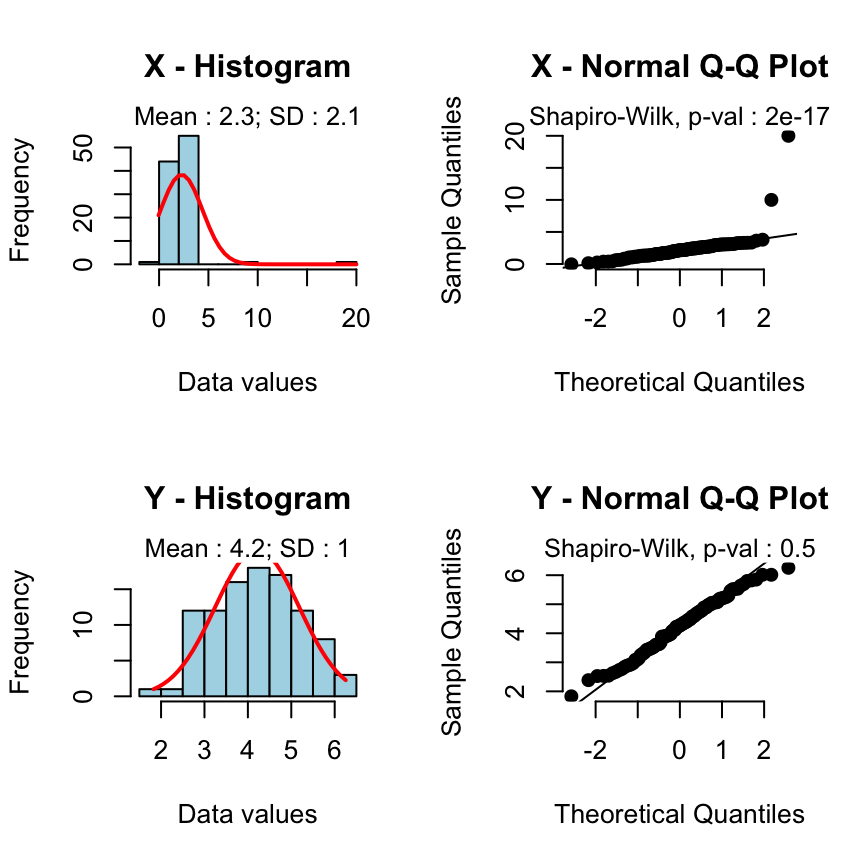
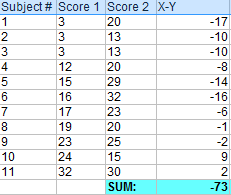
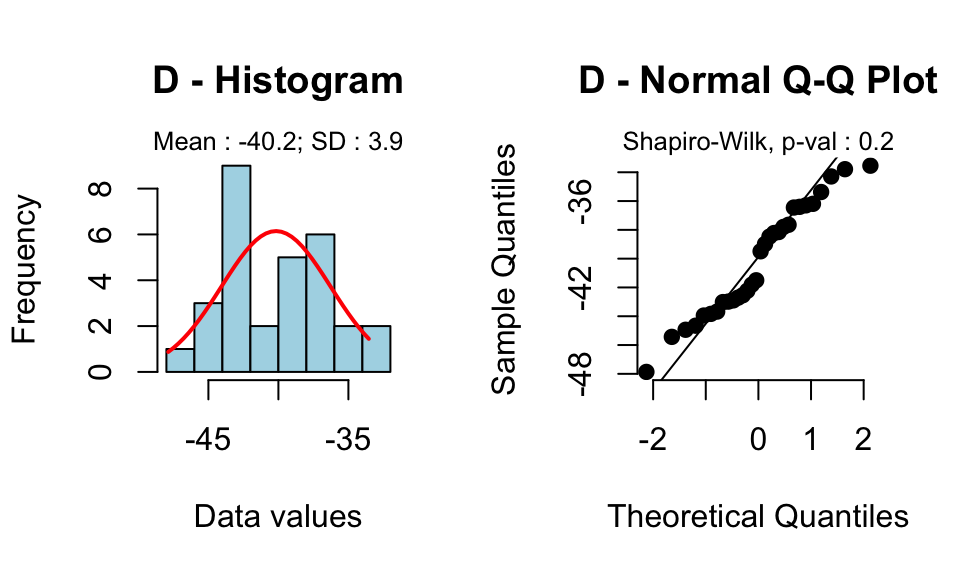
Ttests are handy hypothesis tests in statistics when you want to compare means. You can compare a sample mean to a hypothesized or target value using a onesample ttest. You can compare the means of two groups with a twosample ttest. If you have two groups with paired observations (e. ttest performs a separate ttest along each column and returns a vector For a paired ttest, sd is the standard deviation of x y deviation is unknown. t x s n, where x is the sample mean, is the hypothesized population mean, s is the sample standard deviation, and n is the sample size. This test is known as an a two sample (or unpaired) ttest. It produces a pvalue, which can be used to decide whether there is evidence of a difference between the two population means. The pvalue is the probability that the difference between the sample means is at least as large as what has been observed, under the assumption that the. Sample Size for Paired t Test If possible, choose a range of mean differences that you want have the statistical power to detect. where d deltasd, alpha, 1 power and t v, p is a Student t quantile with v degrees of freedom and probability p. n is rounded up to the closest integer. CIs for the difference between independent means (CI D) and CIs for the difference between paired means (CI PD) can be obtained by using the same formula on the output of the ttest for independentsamples and the pairedsamples ttest, respectively. The paired ttest The output for the standing and supine blood pressure example is shown below, and gives the sample means and the mean difference, their standard deviations and the standard errors. The 95 confidence interval for the mean difference is also shown as well as the ttest of the null hypothesis that the mean difference 0. Since we are trying to estimate a population mean difference in math and English test scores, we use the sample mean difference (d 1) as the sample statistic. In this analysis, the confidence level is defined for us in the problem. The paired sample ttest, sometimes called the dependent sample ttest, is a statistical procedure used to determine whether the mean difference between two sets of observations is zero. In a paired sample t test, each subject or entity is measured twice, resulting in pairs of observations. A paired samples ttest based on a matchedpairs sample results is the sample mean, s is the sample standard deviation of the sample and n is the sample size. The degrees Calc, Microsoft Excel, SAS, SPSS, Stata, DAP, gretl, R, Python, PSPP, Matlab and Minitab, include implementations of Student's ttest. LanguageProgram This project was supported by the National Center for Advancing Translational Sciences, National Institutes of Health, through UCSFCTSI Grant Number UL1 TR. Compute the following values The casewise differences, The mean of the casewise difference, The standard deviation of the casewise differences, The test statistic for the paired ttest. A company markets an eight week long weight loss program and claims that at the end of the program on average a participant will have lost 5 pounds. Paired t Test Menu location: t. This function gives a paired Student t test, confidence intervals for the difference between a pair of means and, optionally, limits of agreement for a pair of samples ( Armitage and Berry, 1994; Altman, 1991 ). Enter the pairs of values obtained for the specimens analyzed by the test method and the comparison method. Number of pairs: 10 20 30 40 50 Note: Resizing SMALLER will lose data higher than the new maximum number of data points. If you have the mean and sd of each group separately then you cannot do it. If you have the mean and sd of the differences and the number of pairs, and are willing to make the necessary assumptions, you can do it, since the formula for the paired ttest is The significance level, or Pvalue, is calculated using the ttest, with the value t calculated as: The Pvalue is the area of the t distribution with n 1 n 2 2 degrees of freedom, that falls outside t (see Values of the t distribution table). Enter either raw data (enter each value) or averaged data (enter mean, N and SD or SEM). If you enter averaged data, you cannot choose a paired t test, which requires raw data. When entering raw data, simply leave a blank spot in the table to denote missing values. I would like to do paired ttest with mean and standard deviation and the number of sampling. 16 number of samples for both AB44 Thanks. I discuss an example of the paireddifference t procedure, working through a confidence interval and hypothesis test and interpreting the results. Ttest Calculator is an online statistics tool for data analysis programmed to calculate the significance of observed differences between the means of two samples when there is null hypothesis that is no significant difference between the means. This calculator generate the Ttest value according to the given two data set inputs of first data set mean and standard deviation and second data set. Assuming that you are trying to test whether there is a significant difference between the mean TASK 1 scores from the mean TASK 2 scores, you would usually use a paired t test (assuming the assumptions hold, esp. Test the mean difference between two samples of continuous data using the 2sample ttest. The calculator uses the probabilities from the student t distribution. For all ttests see the easyT Excel Calculator: : Sample data is available. Effect Size Calculator for t test. Effect size for onesample t test. Mean for H0: Mean for H1: Standard deivation: Calculate 2. Effect size for paired twosample t test. Mean of difference: SD of difference: Calculate 3. Effect size for balancedunbalanced twosample t test. unpaired ttest (also known as the student's ttest) and the paired ttest both assume that analysed data is from a normal distribution unpaired ttest applied to two independent groups e. diabetic patients versus nondiabetics sample size from the two groups may or may not be equal in addition to. The paired samples ttest is used to compare the means between two related groups of samples. In this case, you have two values (i. , pair of values) for the same samples. This article describes how to compute paired samples ttest using R software. t test calculator A t test compares the means of two groups. For example, compare whether systolic blood pressure differs between a control and treated group. Summary: In a paired t test, you find the difference between data pairs. That can be tedious, and its easy to drop a minus sign. That can be tedious, and its easy to drop a minus sign. This page shows you how to use TI8384 list operations to find the differences. Sample Size Estimation and Power Computation on Paired or Skewed Continuous Data March 31, 2006 Power and Sample Size Estimation for paired ttest (for longitudinal followup study). Suppose we are planning a longitudinal (followup) study including 100 Transform published mean and SD for powersample size computation. If you know the mean of the differences, as well as the SD (or SEM) and sample size, you can compute the paired t test. The t ratio equals the mean of the differences divided by the SEM of those differences. These reports include confidence intervals of the mean difference, the paired sample ttest, and nonparametric tests including the randomization test, the quantile (sign) test, and the Wilcoxon Signed This section reports the group name, count, mean, standard deviation, standard error, and confidence interval of the mean for each group. A knowledge of basic statistics is important for the researcher. Paired TTest: This test is used to compare two different groups of data where the observations cannot be categorized into a. The ttest uses a T distribution. It checks if the difference between the means of two groups is statistically correct, based on sample averages and sample standard deviations, assuming unequal standard deviations. Practical MetaAnalysis Effect Size Calculator David B. Means and full sample standard deviation. Mean gains scores and gain score SDs. Mean gain scores, pre and post SDs, and paired ttests. Mean gain scores, pre and post SDs, and prepost r. I know that if I have a set of data, I can run t. But I only know the count, mean and standard deviation for each set. I'm sure there must be a way to do this in R, but I can't figure it out. Yes, you can use a two sample t test to determine whether there is a significant difference between the mean scores of the two groups, provided the assumptions of the t test are met, esp. independent samples and normality (or least not too far from normality). Paired Student's t test Calculator The Paired Student's ttest is a parametric test that determines whether two groups of matched (i. dependent) samples are the same. The greater the mean of the group differences, and the lower the variance of the differences, the higher the calculated t value will be, leading to a lower p. T Test Calculator for 2 Dependent Means The t test for dependent means (also called a repeatedmeasures t test, paired samples t test, matched pairs t test and matched samples t test) is used to compare the means of two sets of scores that are directly related to each other. Dependent TTest using SPSS Statistics Introduction. The dependent ttest (called the pairedsamples ttest in SPSS Statistics) compares the means between two related groups on the same continuous, dependent variable. 1 Paired ttests 1 Introduction A paired ttest is used to compare two population means where you have two samples in which observations in one sample can be paired with observations in the other sample. Paired ttest; Find sample size: If you know the mean difference and its standard deviation, use this form to find the number of subjects you need. Find effect size: If you know the number of subjects and the standard deviation of the change, use this form to find how small a difference you can detect. The ttest works with small or large numbers because it automatically takes into account the number of cases in calculating the probability level. Make use of the below given calculator to calculate the mean difference between matched pairs. T Test Calculator for 2 Dependent Means. The ttest for dependent means (also called a repeatedmeasures ttest, paired samples ttest, matched pairs ttest and matched samples ttest) is used to compare the means of two sets of scores that are directly related to each other. A paired ttest is used to compare two population means where you have two samples in Calculate the standard deviation of the dierences, s d, Calculating the mean and standard deviation of the dierences gives: d 2. Therefore, SE(d) s d n Enter your paired treatment values into the text boxes below, either one score per line or as a comma delimited list. Remember, because the ttest for 2 dependent means uses paired values, you need to have the same number of scores in both treatment conditions. The Pvalue is calculated using the one sample ttest, with the value t calculated as: or when the hypothesized mean is k and the standard deviation is s: The Pvalue is the area of the t distribution with n 1 degrees of freedom, that falls outside t (see Values of the t distribution table). With this T Test Calculator you can calculate all three T Tests at the same time and compare and contrast results. By entering your data into the data set boxes the calculator will automatically calculate the different variables for the sets. A paired difference test uses additional information about the sample that is not present in an ordinary unpaired testing situation, for normally distributed difference ttest (where the population standard deviation of difference is not known) Although the mean difference is the same for the paired and unpaired statistics. Paired ttests can be conducted with the t. test function in the native stats package using the pairedTRUE option. Data can be in long format or short format. Examples of each are shown in this chapter. As a nonparametric alternative to paired ttests, a permutation test can be used. The Student's ttest is used to determine if means of two data sets differ significantly. This calculator will generate a step by step explanation on how to apply t test. The data may either be paired or not paired. By paired, we mean that there is a onetoone correspondence between the values in the two samples. Pooled standard deviation: For our twotailed ttest,.