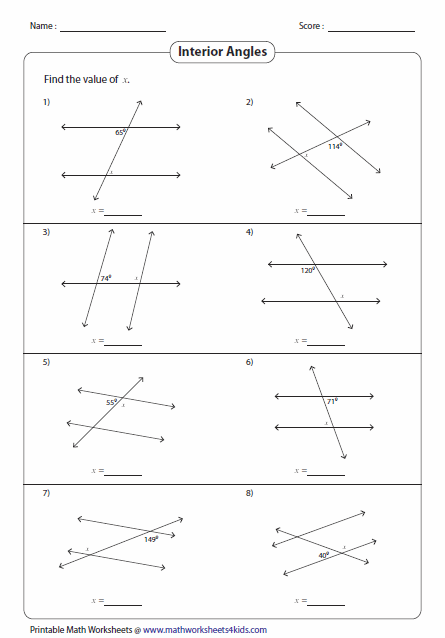
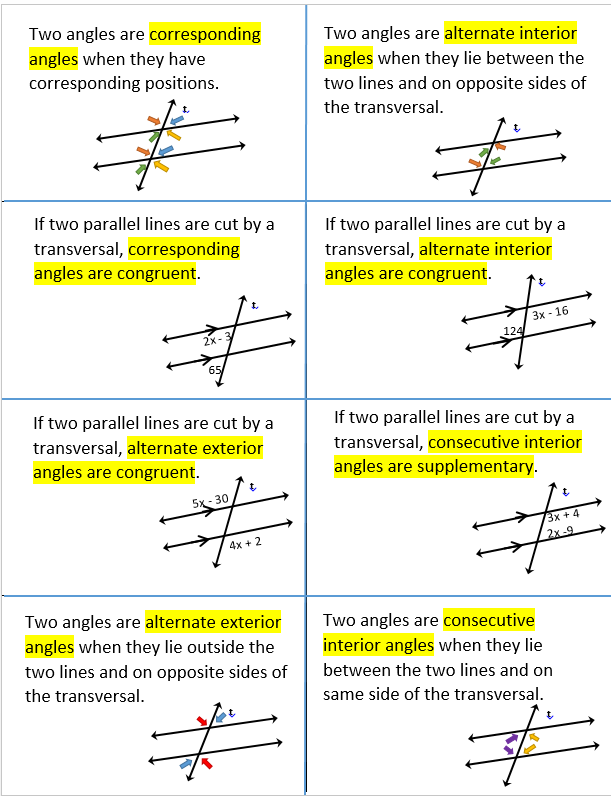
Exterior Algebra nR The exterior algebra Rnconsists of the direct sum from 1 to n of the linear The Cli ord algebra C n is the exterior space Rn C Cli ord algebra that can describe a 4dimensional Minkowski space and the associated rotations. Contents 1 Exterior Calculus page 1 1. 1 Exterior Algebra In this section, we introduce the elements of (multi)linear algebra relevant to this course. algebra, we explicitly describe a g0module Spin 0 (gl) such that the exterior algebra of gl is the tensor square of this module times some power of 2. Although Spin0(h ) is usually reducible. EL LGEBRA GEOMTRICA DEL ESPACIO Y TIEMPO 43 4. EL PRODUCTO EXTERIOR Y SUS APLICACIONES Definicin de producto exterior de vectores Se define el producto exterior de cualquier nmero de vectores como su producto antisimtrico, es decir, el. Di erential Forms Faraad M Armwood North Dakota State September 4, 2016 Faraad M Armwood (North Dakota State) Exterior Algebra! Di erential Forms September 4, 2016 1 17 Document Viewer Online [EBook PDF EPUB Tensor Spaces And Exterior Algebra Tensor Spaces And Exterior Algebra In this site is not the same as a answer manual you purchase in a stamp An exterior algebra may also be defined for more general objects, viz. for unitary modules over a commutative ring with identity. The th exterior power, , of a module is defined as the quotient module of the th tensor power of this module by the submodule generated by the elements of the form. 2 De nitions, uniqueness, existence 28. 4 Exterior powers V i fof maps 28. 5 Exterior powers of free modules f 0N1a 'H Kq NV1a KB010d01. KB010cIo saoecls pue 'ATIrIVHS ' uo ONVHO pp01N snonunuoo suvqvcl. O 50 'ugaxvqsnv snoauafi0L110H uo algebra. Tensor, Exterior and Symmetric Algebras. eclipse modeling project a domain specific language dsl toolkit pdf download Throughout this note R is a commutative ring, all modules are left Rmodules. 4 HOCHSCHILD COHOMOLOGY OF THE EXTERIOR ALGEBRA 2. Preliminaries Throughout, kis a eld of characteristic 0 and k. We use the notation V for Homk(V, k) if V is a nite dimensional kvector space, for isomorphism, and for quasi isomorphism. The alternating algebra, also called the exterior algebra, is a dimensional algebra. In the Wolfram Language, an element of the alternating algebra can be represented by an nested binary list. For example, 1, 2, 0, 0, 3, 0, 4, 5 represents. 114 Chapter VIII: Exterior Algebra Now assurne, by induction, that (8. 4) is correct for a permutation a which is the product of N transpositions. Consider the permutation Study on Exterior Algebra Bundle and Differential Forms 201 each 0 I, if d, , df is a basis of I, then the set ghdi j di k l 1mD: D0 m E is a basis of 0 I. The \th exterior bundle over (smooth manifold) is the vector bundle 0 0 n o p o q product is the exterior product. The exterior algebra provides an algebraic setting in which to answer geometric questions. For instance, blades have a concrete geometric interpretation, and objects in the exterior algebra can The Geometry of the Dot and Cross Products. Exterior algebra is not any more superior to linear algebra than multiplication is superior to addition. Both are important, there are important connections between the two, and you definitely need to understand addition first before you understand multiplication. GUIA DE ALGEBRA DIRECTOR Remigio Castelln Alvarado SUBDIRECTOR Sergio Prez Njera The structure of the exterior algebra kRn is studied in low dimensions, and consequences are drawn for kdimensional areaminimizing surfaces in Rn. Tensor, Exterior and Symmetric Algebras Daniel Murfet May 16, 2006 3 The Exterior Algebra 6 4 The Symmetric Algebra 19 1 Denitions Denition 1. A Ralgebra is a ring morphism: R Awhere Ais a ring and the image of is contained in the center of A. (2007), Grassmann algebra Exploring applications of Extended Vector Algebra with Mathematica, Published on line An introduction to the exterior algebra, and geometric algebra, with a focus on applications. Sheaf Algorithms Using the Exterior Algebra Wolfram Decker and David Eisenbud In this chapter we explain constructive methods for computing the cohomol 2 Linear Algebra Michael Taylor 21. Exterior algebra Isomorphism Skew(V) 2V and the Pfaan22. Vector spaces over more general elds 23. Rings and modules Modules over a PID 24. The Jordan canonical form revisited Vol. 34, 1980 393 Exterior algebra representations of commutative Moufang loops By g. Exterior algebra or assoeiator calculus. PDF This note surveys how the exterior algebra and deformations or quotients of it, gives rise to centrally important notions in five domains of mathematics: Combinatorics, Topology, Lie theory. Exterior algebra structure on relative invariants M with respect to M. WehavenH() 0, so a hyperplane of a low multiplicity with respect to M and is always of a low multiplicity with respect to M. Let us assume that H is an hyperplane which is reectionpre The exterior algebra V \Lambda V of a vector space is the free gradedcommutative algebra over V V, where the elements of V V are taken to be of degree 1 1. (That is, the forgetful functor takes a gradedcommutative algebra to its vector space of degree 1 1 elements. ) Fundamentals of Grassmann Algebra Eric Lengyel, PhD Terathon Software. Math used in 3D programming The exterior product needed for these notes is mostly linear algebra (of the geometric kind; vector spaces and linear transformations in preference to column vectors and matrices, although the latter are used too). exterior power of the vector space to the vector space. Property (b) is called the Jacobi identity; it is related to the usual asso Exterior powers also arise in representation theory, as one of several ways of creating new representations of a group from a given representation of the group. Algebra, Topology, Differential Calculus, and Optimization. 2 Introduction Geometric algebra is the Cli ord algebra of a nite dimensional vector space over real scalars cast in a form most appropriate for physics and engineering. Preface In a rst course of linear algebra, one learns the various uses of matrices, for instance the properties of determinants, eigenvectors and eigenvalues, and Read the latest articles of Journal of Algebra at ScienceDirect. com, Elseviers leading platform of peerreviewed scholarly literature Introduction to the Grassmann Algebra and Exterior Products. September 3, 2012 jmanton Leave a comment Go to comments. The exterior algebra of a vector space is a vector space whose elements represent equivalence classes of linear combinations of oriented parallelotopes in. Geometric Algebra and its Application to Mathematical Physics Chris J. Doran Sidney Sussex College A dissertation submitted for the degree of Doctor of Philosophy in the University of Parallel Lines and Transversals Date Period Identify each pair of angles as corresponding, alternate interior, alternate exterior, or consecutive interior. 1) Microsoft Word Worksheet Triangle sum and exterior angle. doc Author: JSCHROE1 Created Date: 6: 16: 13 PM. THE WEDGE PRODUCT FOR SOPHOMORE CALCULUS FRANK BIRTEL The exterior algebra oers a computational and conceptual tool which can be introduced in sophomore multivariable calculus with a minimum of formalism. tensor algebras, central simple algebras and the Brauer group, exterior algebra (including Grassmann algebras and the binomial theorem), determinants, differential forms, and an. Chapter 22 Tensor Algebras, Symmetric Algebras and Exterior Algebras 22. 1 Tensors Products We begin by dening tensor products of vector spaces over a eld and then we investigate Linear Algebra via Exterior Products Paperback January 4, 2010. The author is also to be praised for making this book available FREE as a PDF file on the web in these days where students in the UK pay more than ever for tuition, every little saving must help. The Exterior Algebra and Central Notions in Mathematics Gunnar Flystad Dedicated to Stein Arild Strmme ( ) The neglect of the exterior algebra is the The Exterior Angle Theorem Date Period Find the measure of each angle indicated. Notes on Tensor Products and the Exterior Algebra For Math 245 K. Purbhoo July 16, 2012 1 Tensor Products 1. 1 Axiomatic de nition of the tensor product Survey on exterior algebra and di erential forms Daniel Grieser 16. Mai 2013 Inhaltsverzeichnis 1 Exterior algebra for a vector space 1 1. Notes on Linear Algebra Mark Reeder December 19, 2015 Contents I The Tensor Algebra and its quotients3 1 The Tensor Algebra3 The exterior algebra ( M) is the Ralgebra obtained as the quotient of T(M) by the homogeneous ideal I alt(M) generated by fm m: m2Mg. Finite element exterior calculus, homological techniques, and applications and homological algebra to develop discretizations which are compatible with the geometric, topological, and algebraic structures which underlie wellposedness of the PDE problem being solved. This is one of over 2, 200 courses on OCW. Find materials for this course in the pages linked along the left. MIT OpenCourseWare is a free open publication of material from thousands of MIT courses, covering the entire MIT curriculum..